I love Streamlit. I moved most of my content, websites, and code to Streamlit to make it more interactive. Recently, I presented at PyCon Chile using Streamlit as a PowerPoint substitute. But as my content grew, handling different "pages" got complicated. I had to copy-paste the page handling code from one repository to another. I wanted a simple solution that any person, especially teachers, could use to create an interactive app for teaching or self-learning. Let people focus on the content and the technology takes care of the rest!
After some thought, I realized that the best way to solve this was to create a companion library for Streamlit. I called it streamlit_book. I coded it to take all of the bookkeeping (pun intended!). I even defined some Markdown formats and Python functions so you can do quizzes more easily: true/false questions, multiple-choice, single-choice, and others. You can put your content on plain Markdown, or you take advantage of the interactivity provided by Streamlit and Python, it's up to you!
In this post, I'll show you how to use the library to create interactive books or presentations with Streamlit:
- Install the library
- Create the main file
- Create content in Markdown files
- Create content in Python file
- Share your app!
You can take a sneak peek at the app here and see the docs here.
Install the library
Let's build a short tutorial called "Happy Birds". It'll teach you how to win at a game involving flying birds, pigs, and trajectories. As usual, store all the required libraries in your app in a file requirements.txt:
streamlit
streamlit_book
matplotlib
numpy
Install these libraries using pip (or use a different virtual environment):
pip install -r requirements.txt
Create the main file
Create a file happy_birds.py and define the properties:
import streamlit as st
import streamlit_book as stb
# Streamlit webpage properties
st.set_page_config(page_title="HappyBirds", page_icon="🐦")
# Streamlit book properties
stb.set_book_config(path="HappyBirds")
- Lines 1 and 2 are regular library imports.
- Line 5 sets up the Streamlit app. You can use all the regular Streamlit magic here: set up the layout, the page title (on your browser's tab), and even a small icon.
- Line 8 sets up Streamlit Book by indicating a folder where it should look for content files. Make sure to create the folder HappyBirds.
If you run the file happy_birds, it'll show a warning message of having no content files:
streamlit run happy_birds.py
Create content in Markdown files
Create content by adding files into the folder HappyBirds. Notice that Streamlit Book will sort the files using lexicographic (alphabetic) order, so it can be helpful to put numbers before the names to have the desired ordering.
First, create "00 Cover.md." This file will be a cover image for the book, with a big image and some funny text to engage readers:
# Happy Birds
This web app illustrates the use of [streamlit_book](<https://streamlit-book.readthedocs.io/en/latest/>) for teaching and learning. In this particular web app, we will explain motion trajectories.
<img src="<https://github.com/sebastiandres/streamlit_happy_birds/blob/main/images/happybird.png?raw=true>" alt="happy Birds" width="700">
Happy Birds uses streamlit, streamlit book, numpy and matplotlib libraries.
Notice that you need to insert the URL of the image, not the local path.
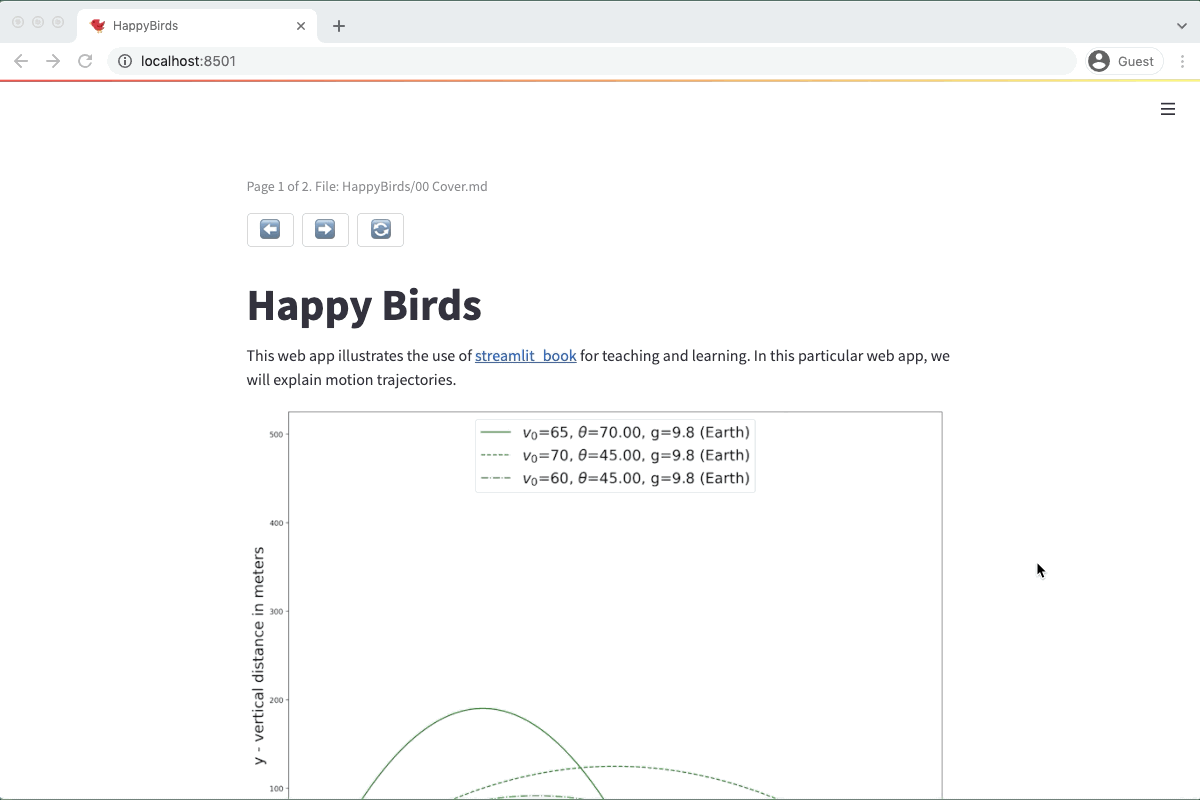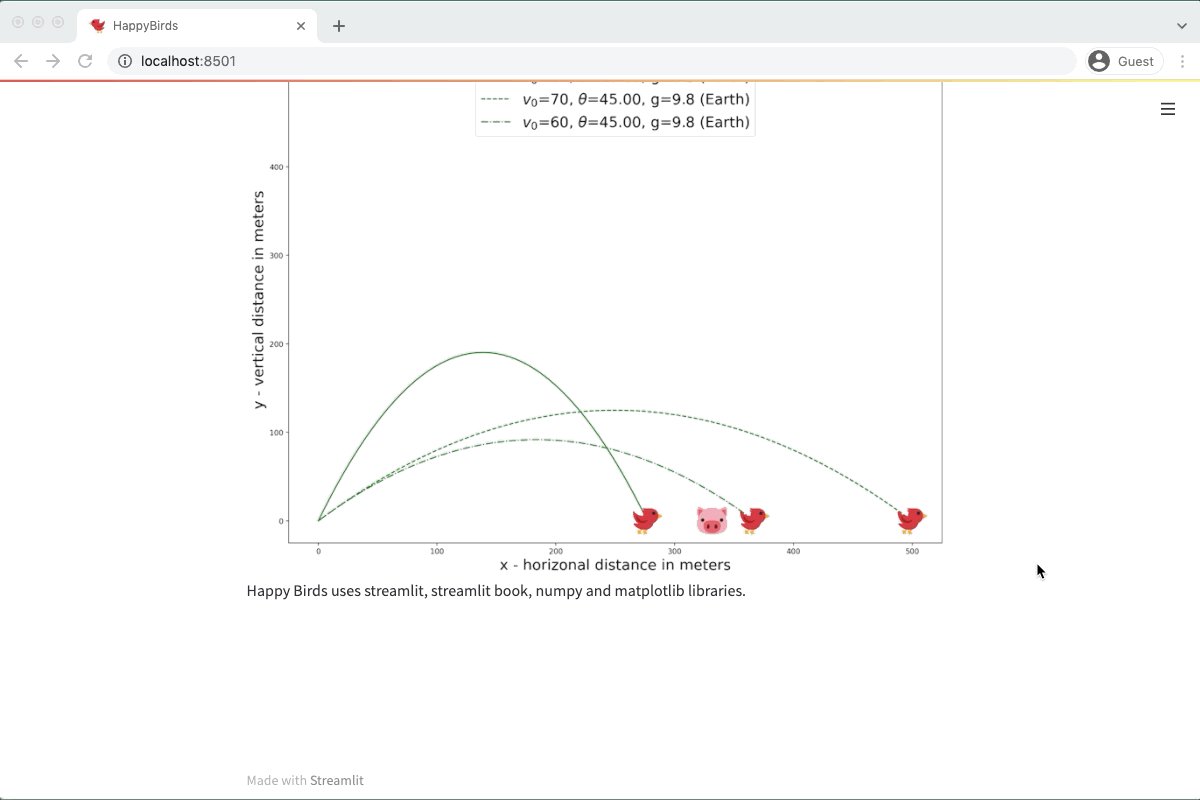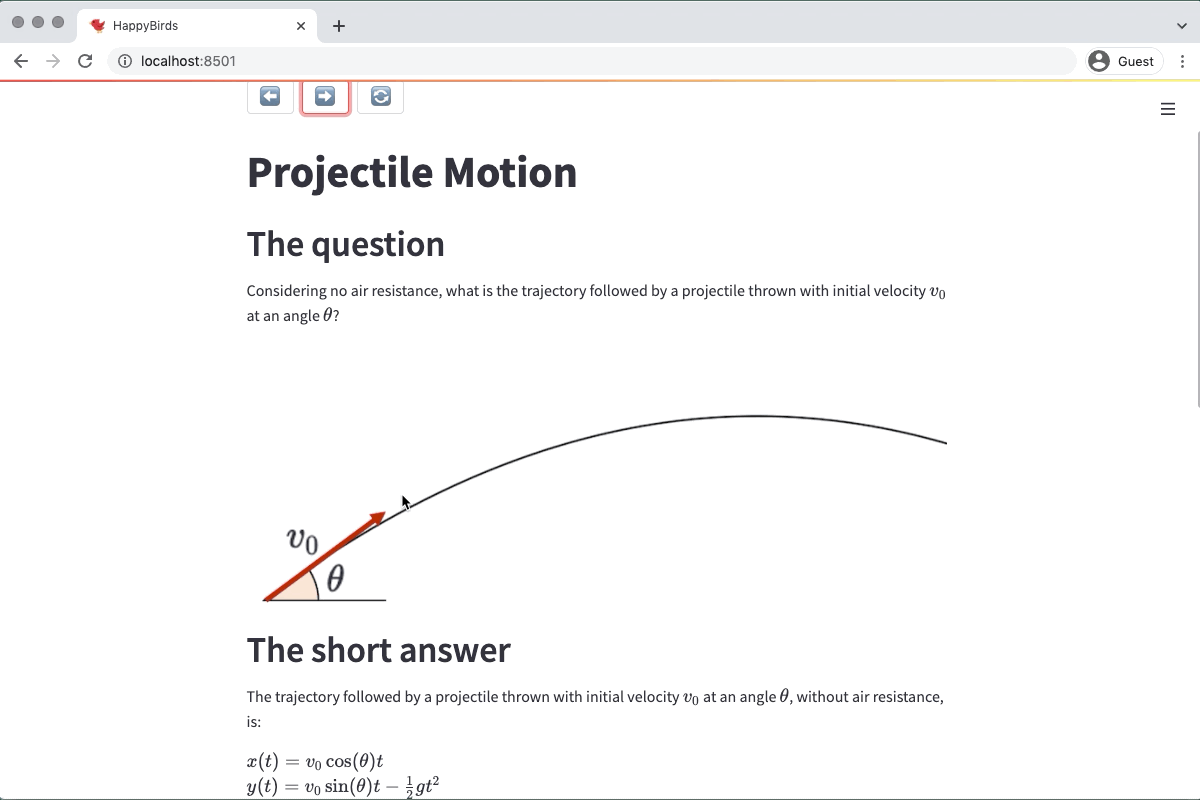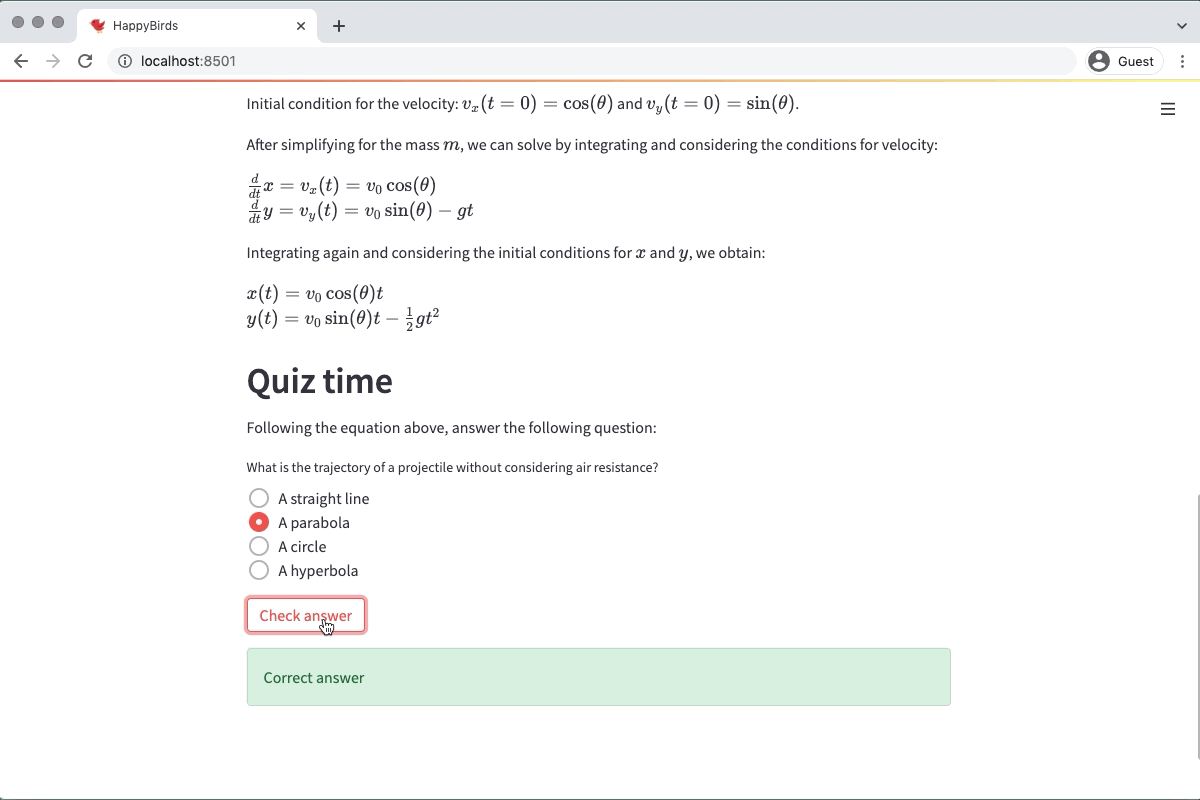
Next, create "01 The Theory.md". This is the file with the (hopefully not boring) explanations of how projectile motion works. Notice how we put a quiz at the end!
# Projectile Motion
## The question
Considering no air resistance, what is the trajectory followed by a projectile thrown with initial velocity $v_0$ at an angle $\\theta$?
<img src="<https://github.com/sebastiandres/streamlit_happy_birds/blob/main/images/definition.png?raw=true>" alt="Parameter Definition" width="700">
## The short answer
The trajectory followed by a projectile thrown with initial velocity $v_0$ at an angle $\\theta$, without air resistance, is:
$$
x(t) = v_0 \\cos(\\theta)t \\\\\\\\
y(t) = v_0 \\sin(\\theta)t - \\frac{1}{2} g t^{2}
$$
where $x$ and $y$ are the horizontal and vertical directions, and $g$ is the acceleration due to gravity.
## The long answer
To obtain the trajectory we start with the equations for the acceleration as given by Newton's Laws:
$$
m \\frac{d^{2}}{dt^{2}} x = 0 \\\\\\\\
m \\frac{d^{2}}{dt^{2}} y = - mg
$$
Initial condition for the position: $x(t=0)=0$ and $y(t=0)=0$.
Initial condition for the velocity: $v_x(t=0) = \\cos(\\theta)$ and $v_y(t=0) = \\sin(\\theta)$.
After simplifying for the mass $m$, we can solve by integrating and considering the conditions for velocity:
$$
\\frac{d}{dt}x = v_x(t)= v_0 \\cos(\\theta) \\\\\\\\
\\frac{d}{dt}y = v_y(t)= v_0 \\sin(\\theta) - g t
$$
Integrating again and considering the initial conditions for $x$ and $y$, we obtain:
$$
x(t) = v_0 \\cos(\\theta)t \\\\\\\\
y(t) = v_0 \\sin(\\theta)t - \\frac{1}{2} g t^{2}
$$
## Quiz time
Following the equation above, answer the following question:
stb.single_choice
What is the trajectory of a projectile without considering air resistance?
- A straight line
+ A parabola
- A circle
- A hyperbola
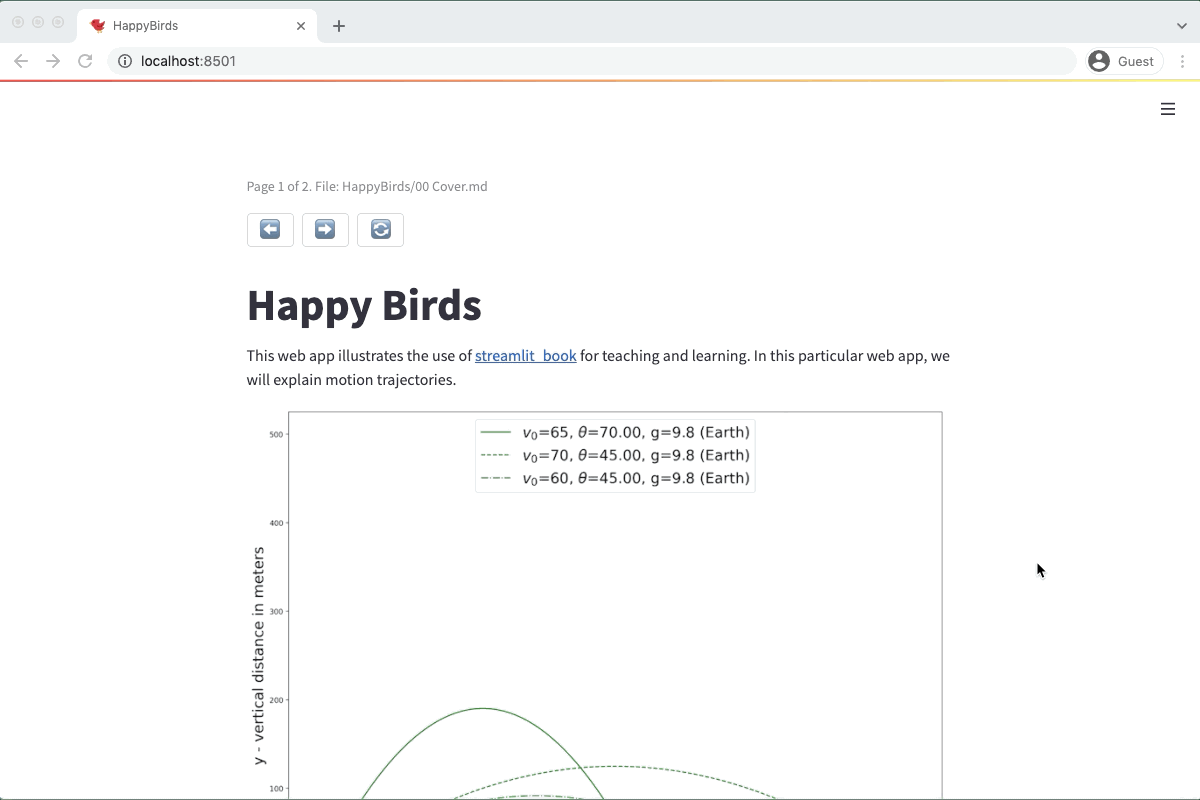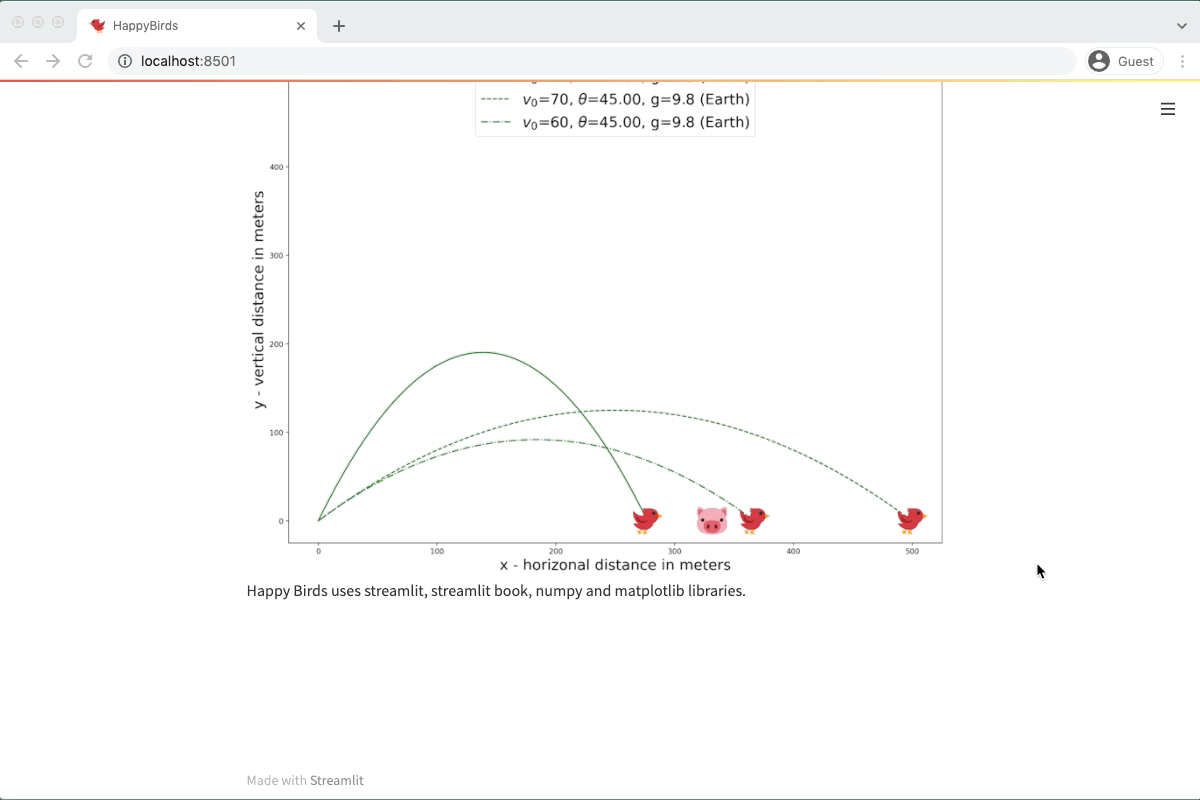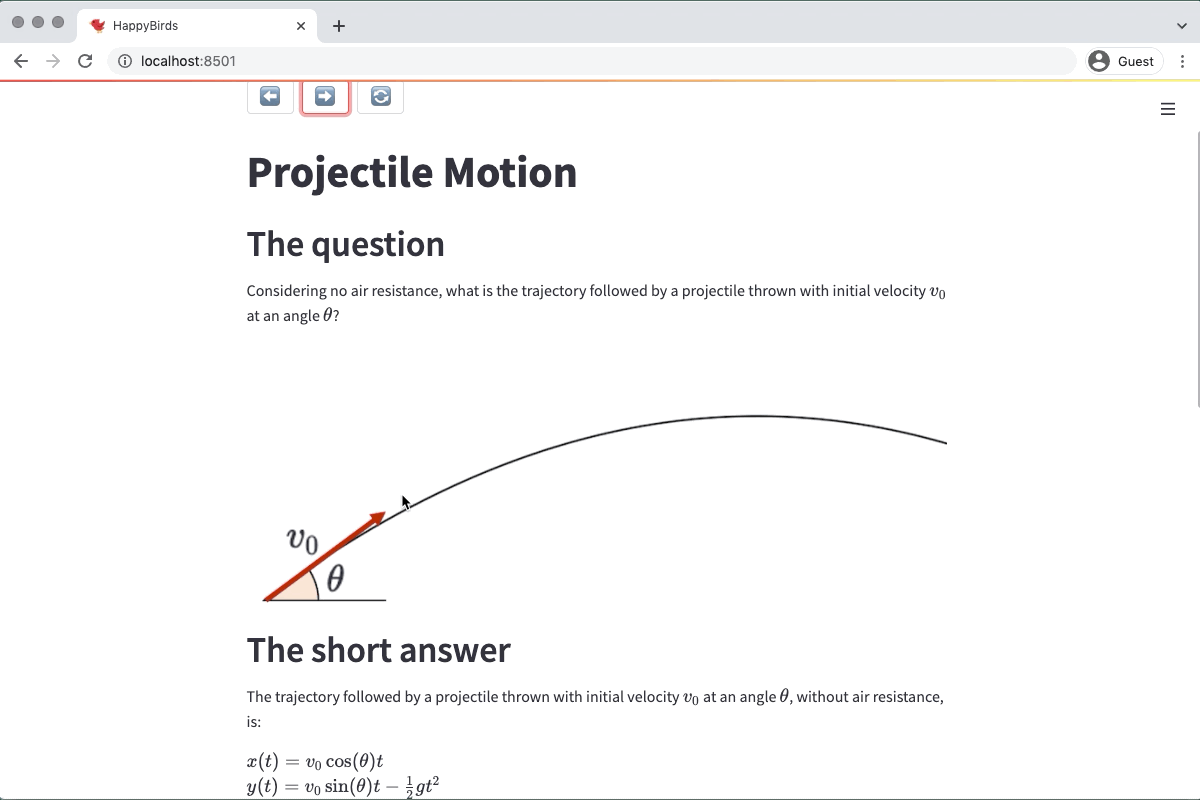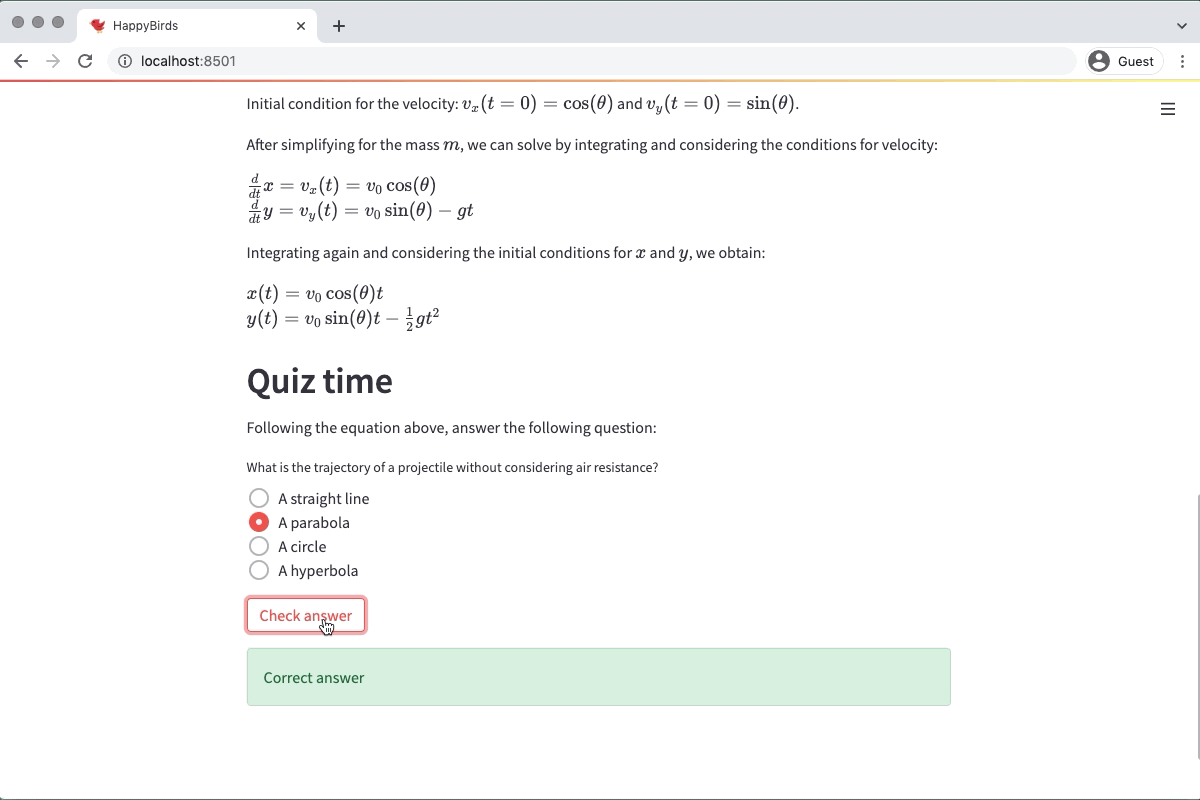
The Streamlit + Streamlit Book app will update automatically, and you'll be able to navigate the created pages.
Create content in a Python file
Now, let's add an interactive page for people so people can try different parameters. You can even use questions from streamlit_book! Call this file "02 The practice.py":
import streamlit as st
import streamlit_book as stb
import numpy as np
from code.trajectory import get_trajectory, fig_from_list
if "trayectory_list" not in st.session_state:
st.session_state["trayectory_list"] = []
# Title
st.title("Trajectory of a projectile")
st.subheader("Equations of motion of a projectile")
st.latex("x(t) = v_0 \\\\cos(\\\\theta)t")
st.latex("y(t) = v_0 \\\\sin(\\\\theta)t - \\\\frac{1}{2} g t^{2}")
# Parameters
st.subheader("Simulation parameters")
c1, c2, c3 = st.columns(3)
dv0 = 1
v0 = c1.slider("Initial Velocity [meters/second]",
min_value=dv0, max_value=100*dv0,
value=10*dv0, step=dv0, help="Initial velocity for the projectile")
dtheta = 1
theta_deg = c2.slider("Initial Angle [degrees]",
min_value=5, max_value=90,
value=45, step=5, help="Initial velocity for the projectile")
# options for gravity: earth, moon, mars, jupiter
gravity_dict = {'Earth': 9.8, 'Moon': 1.6, 'Mars': 3.7, 'Jupiter': 24.8}
gravity_label = c3.selectbox("Gravity", gravity_dict.keys(), index=0)
gravity = gravity_dict[gravity_label]
# Compute the plot
c1, c2 = st.columns([.5, .1])
if c1.button("Add plot"):
traj_dict = get_trajectory(v0, theta_deg, gravity, gravity_label)
st.session_state["trayectory_list"].append(traj_dict)
if c2.button("Clear plots"):
st.session_state["trayectory_list"] = []
if len(st.session_state["trayectory_list"]) > 0:
fig = fig_from_list(st.session_state["trayectory_list"])
st.pyplot(fig)
# The quizz
st.subheader("Quizz time!")
stb.single_choice("At what angle is obtained the maximal distance?",
options=["15", "30", "45", "60", "75"], answer_index=2)
stb.true_or_false("On the moon, the horizontal distance is always larger than on the earth under the same initial velocity and angle.",
answer=True)
This makes use of some helper functions in code/trajectories.py. Everything is on the GitHub repo.
Let's make it fun!
We can even make a game out of it, to further test people's understanding of the motion equations.
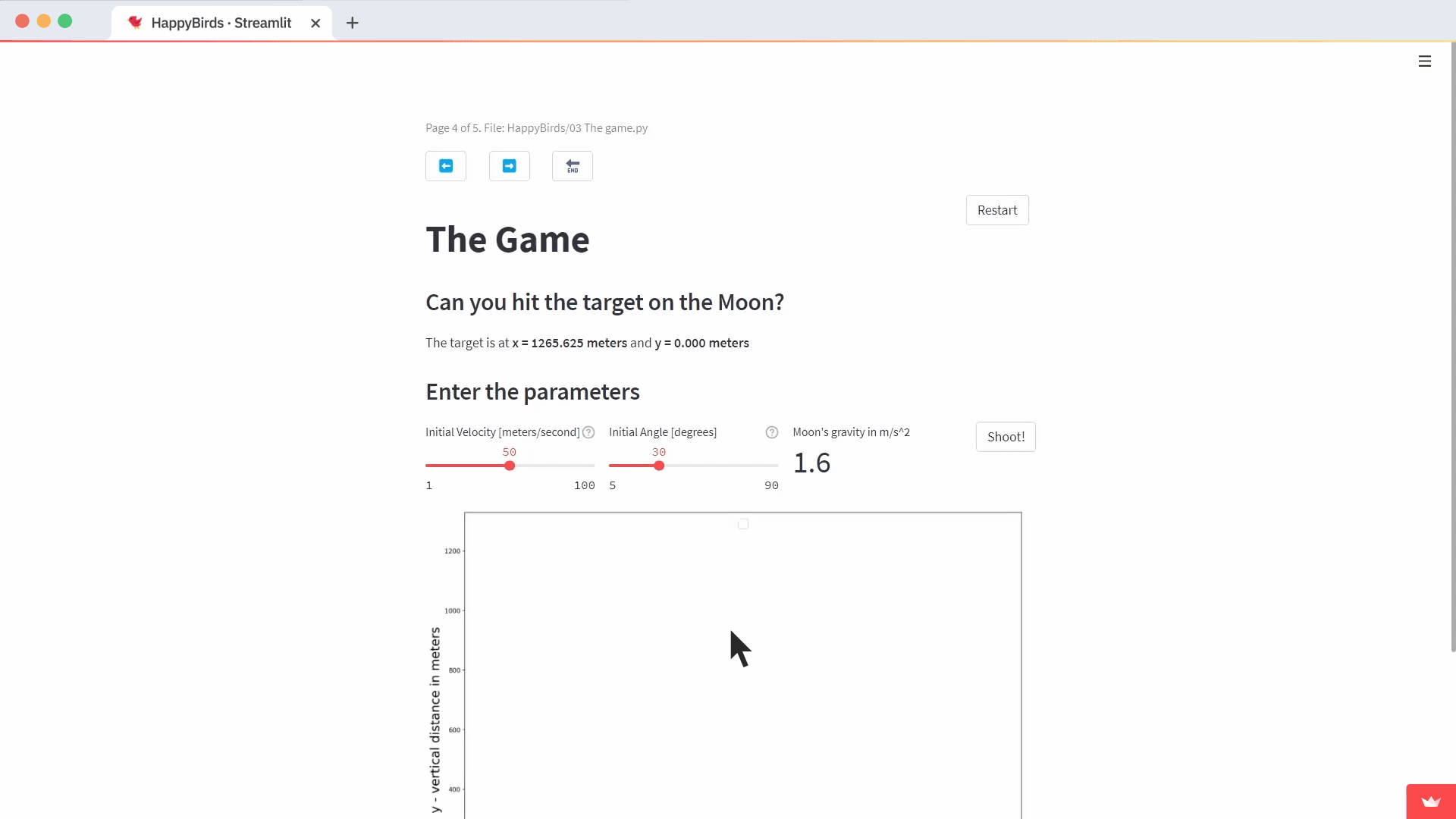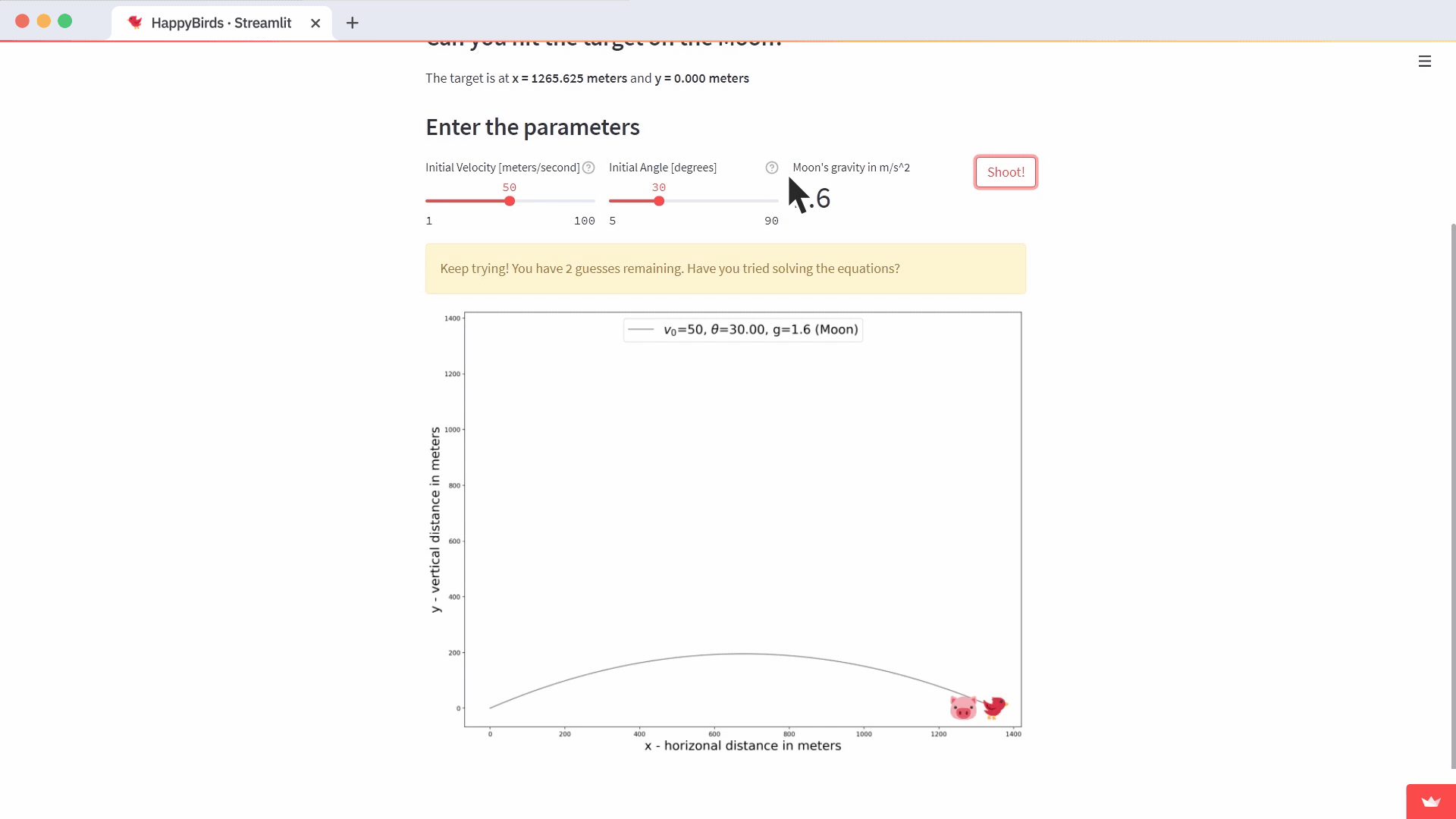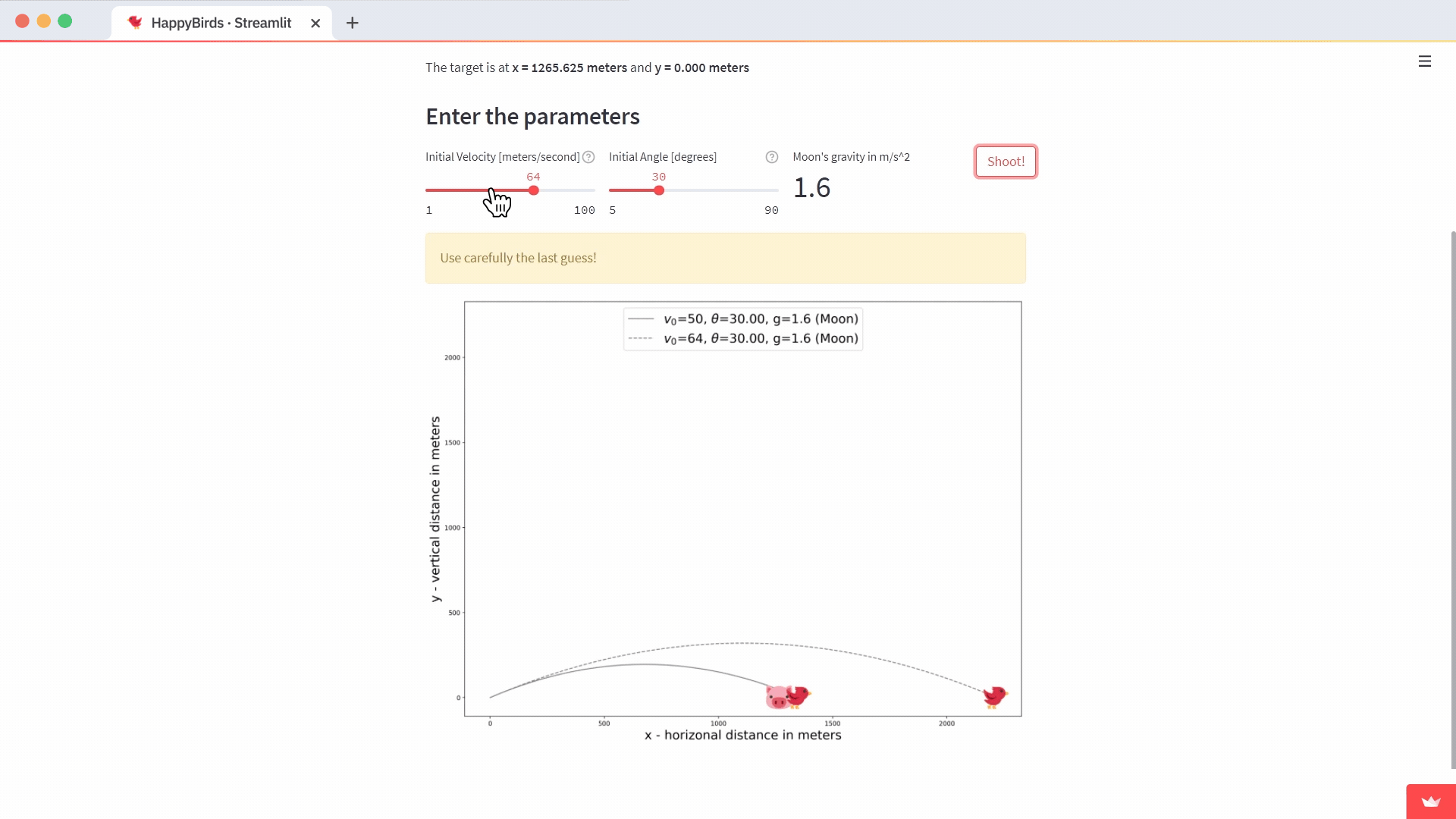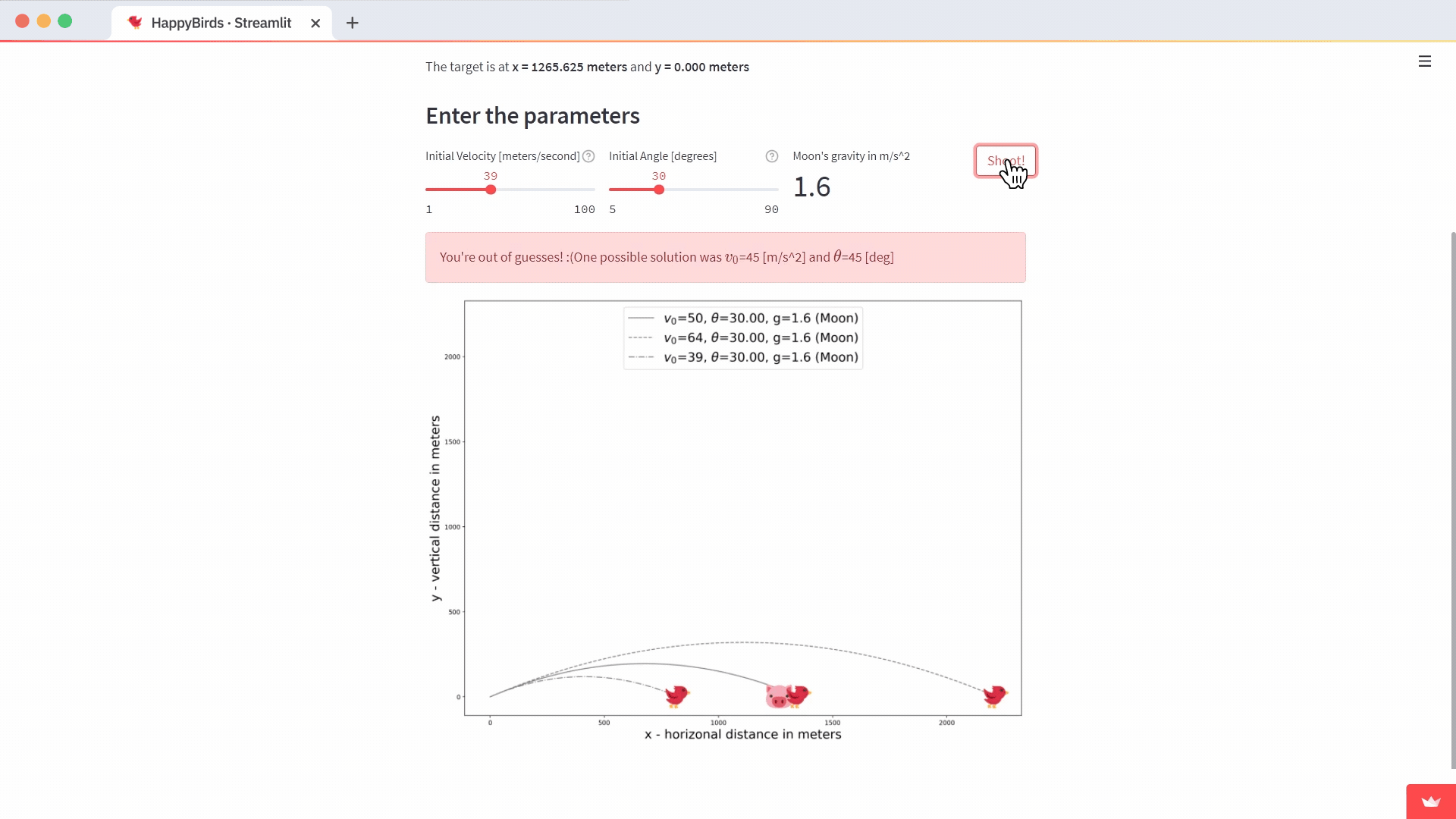
Let's create a "03 The game.py" file with the content.
import streamlit as st
import numpy as np
from code.trajectory import get_trajectory, fig_from_list, check_solution
# Fill up the page
c1, c2 = st.columns([8,1])
c1.title("The Game")
restart = c2.button("Restart")
# Gravity constants by planet
GRAVITY_DICT = {'Earth': 9.8, 'Moon': 1.6, 'Mars': 3.7, 'Jupiter': 24.8}
# Setup the session_state variables
if restart or "remaining_guesses" not in st.session_state:
st.session_state["remaining_guesses"] = 3
if restart or"guess_list" not in st.session_state:
st.session_state["guess_list"] = []
if restart or"game_gravity_index" not in st.session_state:
st.session_state["game_gravity_index"] = np.random.randint(0, len(GRAVITY_DICT))
planet_list = list(GRAVITY_DICT.keys())
game_planet = planet_list[st.session_state["game_gravity_index"]]
game_gravity = GRAVITY_DICT[game_planet]
if restart or "solution" not in st.session_state:
v0_sol = np.random.randint(30, 60)
theta_deg_sol = 45
theta_rad_sol = theta_deg_sol * np.pi / 180
t_max_sol = 2*v0_sol*np.sin(theta_rad_sol)/game_gravity
x_max_sol = v0_sol*np.cos(theta_rad_sol)*t_max_sol
pig_position = [x_max_sol, 0]
st.session_state["solution"] = {
"pig_position":pig_position,
"v0_sol": v0_sol,
"theta_deg_sol": theta_deg_sol,
}
article_dict = {'Earth': "", 'Moon': "the", 'Mars': "", 'Jupiter': ""}
c1.subheader(f"Can you hit the target on {article_dict[game_planet]} {game_planet}?")
# Pig position
x_text = f"x = {st.session_state.solution['pig_position'][0]:.3f} meters"
y_text = f"y = {st.session_state.solution['pig_position'][1]:.3f} meters"
st.write(f"The target is at **{x_text}** and **{y_text}**")
# Get the parameters
st.subheader("Enter the parameters")
c1, c2, c3, c4 = st.columns([3,3,3,1])
dv0 = 1
v0 = c1.slider("Initial Velocity [meters/second]",
min_value=dv0, max_value=100*dv0,
value=50, step=dv0, help="Initial velocity for the projectile")
dtheta = 1
theta_deg = c2.slider("Initial Angle [degrees]",
min_value=5, max_value=90,
value=30, step=5, help="Initial velocity for the projectile")
# options for gravity: earth, moon, mars, jupiter
c3.metric(value=game_gravity, label=f"{game_planet}'s gravity in m/s^2")
# Shoooooot
if st.session_state["remaining_guesses"] > 0:
if c4.button("Shoot!"):
st.session_state["remaining_guesses"] -= 1
traj_dict = get_trajectory(v0, theta_deg, game_gravity, game_planet)
st.session_state["guess_list"].append(traj_dict)
# Placeholder for information
placeholder = st.empty()
# Always plot, to show the target
fig = fig_from_list(st.session_state["guess_list"], st.session_state.solution["pig_position"])
st.pyplot(fig)
# We check if we hit the pig after the shoot we have guesses left
if check_solution(st.session_state.solution["pig_position"], st.session_state["guess_list"]):
placeholder.success("You hit the pig... I mean, the target!")
elif st.session_state["remaining_guesses"] == 0:
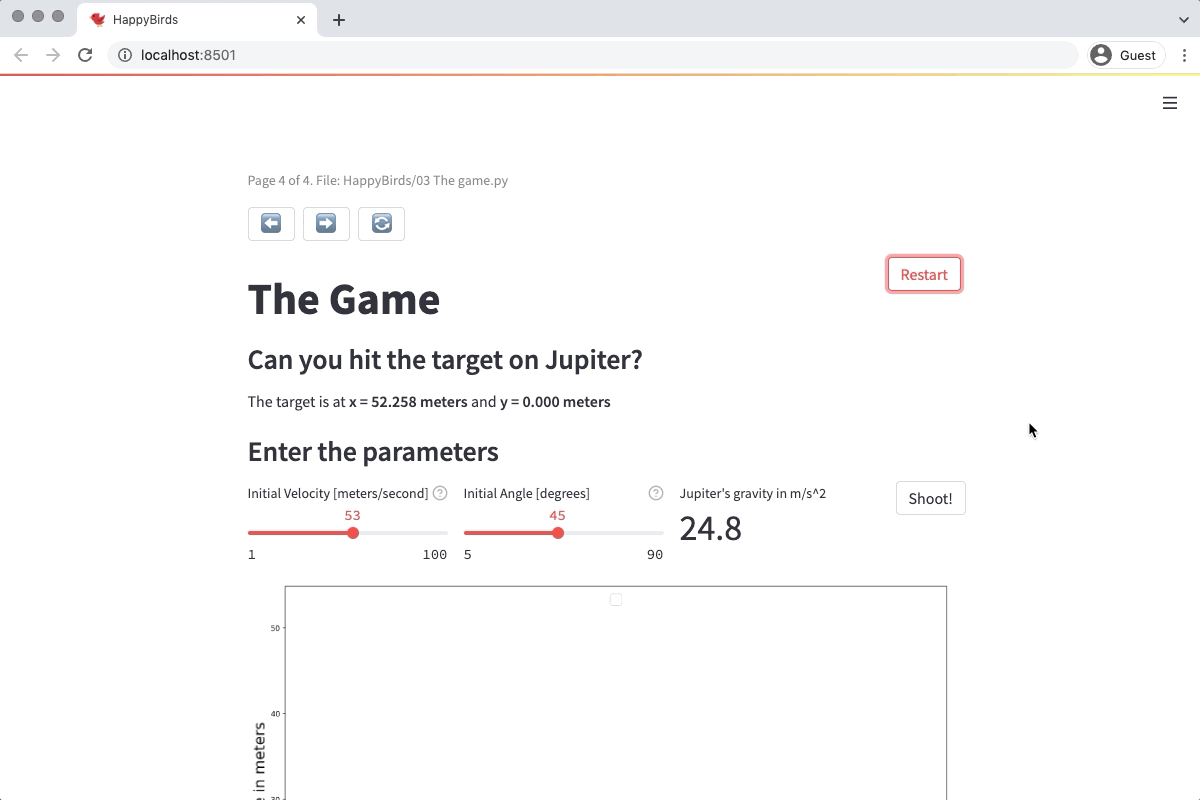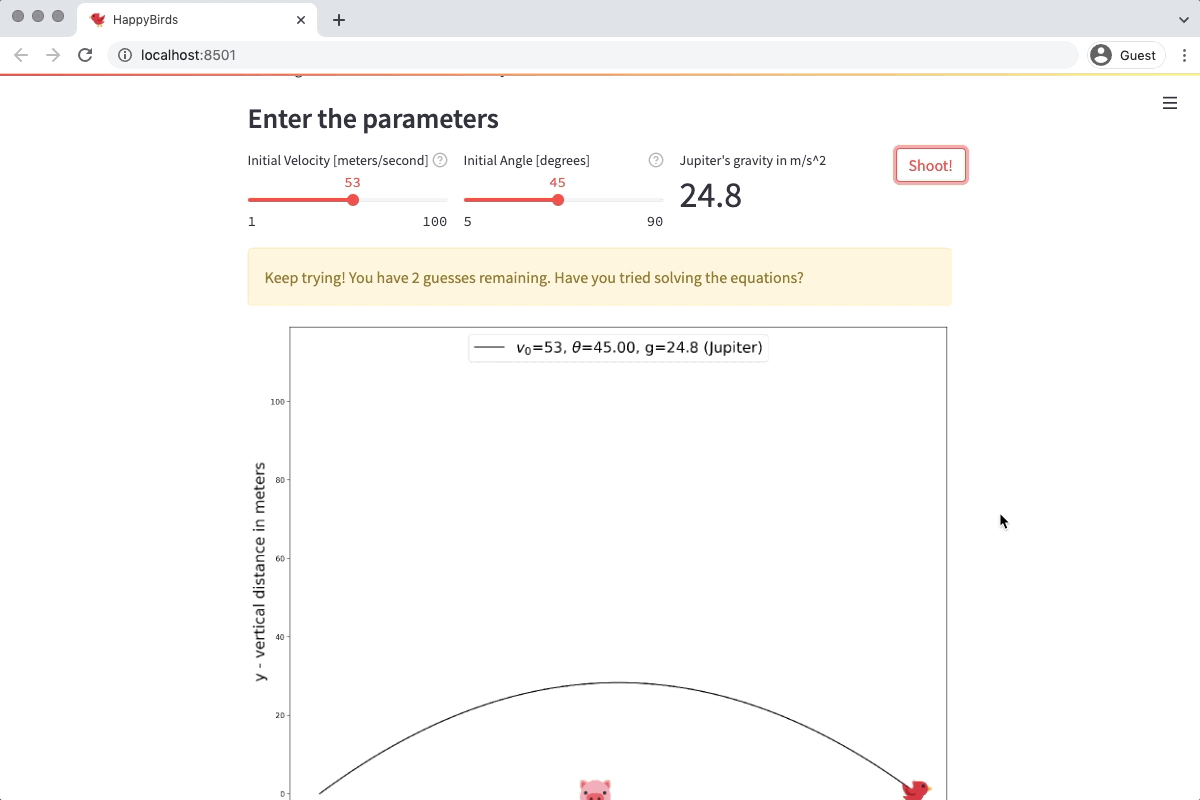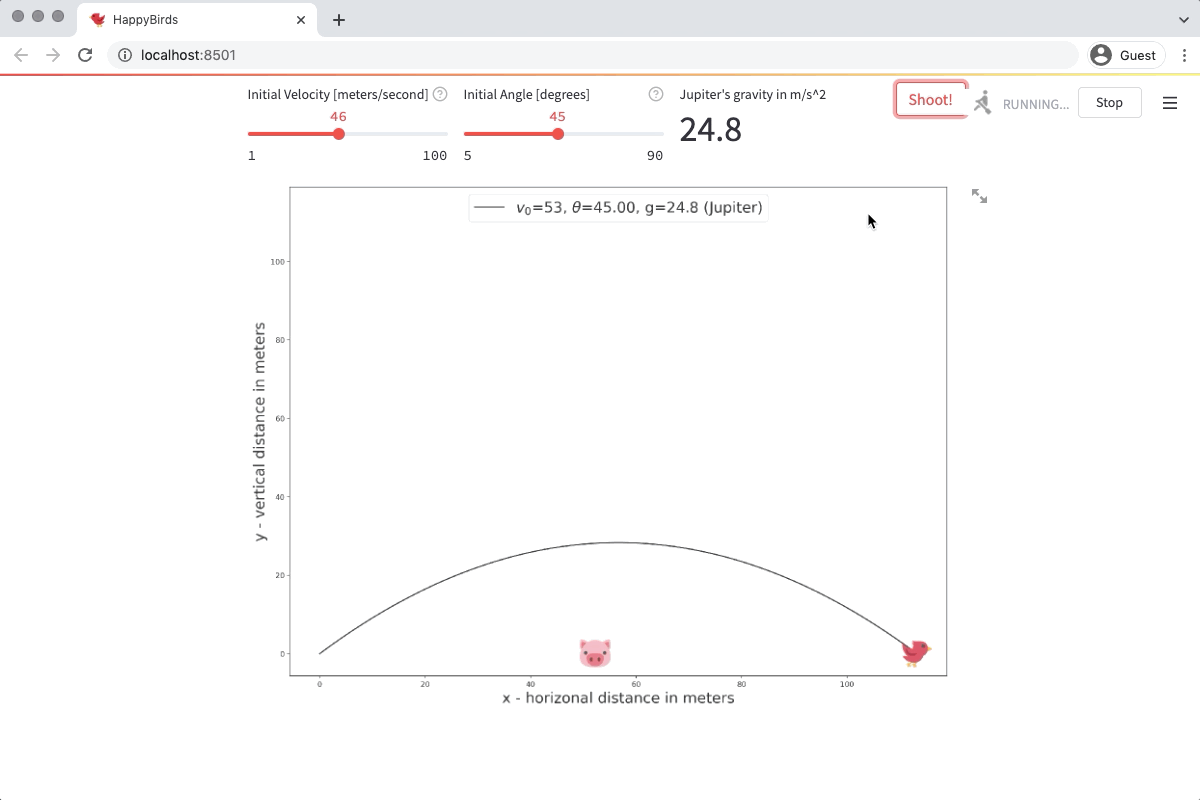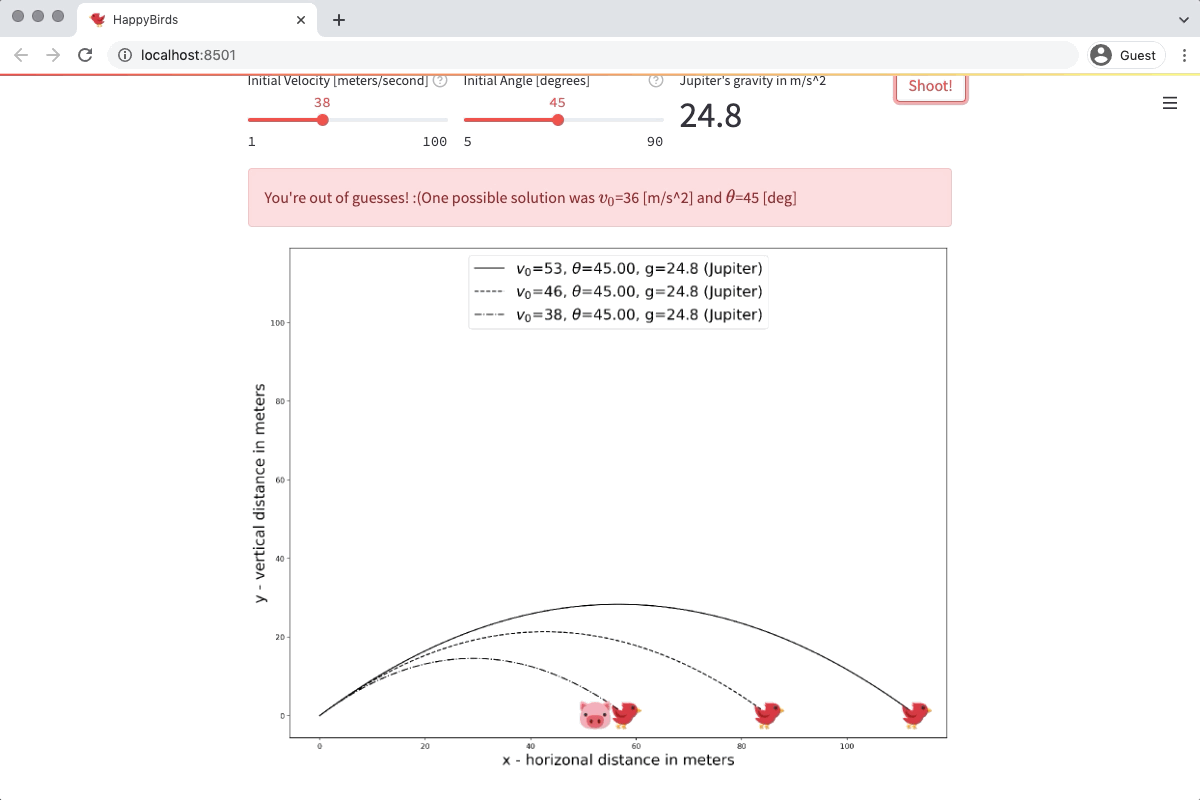
line1 = "You're out of guesses! :("
v0_sol = st.session_state.solution["v0_sol"]
theta_deg_sol = st.session_state.solution["theta_deg_sol"]
line2 = f"One possible solution was $v_0$={v0_sol} [m/s^2] and $\\\\theta$={theta_deg_sol} [deg]"
placeholder.error(line1 + line2)
else:
# Say to keep trying, but only if at least tried once
if st.session_state['remaining_guesses']==2:
text = f"Keep trying! You have {st.session_state['remaining_guesses']} guesses remaining. Have you tried solving the equations?"
placeholder.warning(text)
if st.session_state['remaining_guesses']==1:
text = f"Use carefully the last guess!"
placeholder.warning(text)
Share your app!
Finally, you can share your app with the world (and your students!). It's as easy as sharing any Streamlit app, because streamlit_book is just another required library.
Wrapping up
I had a lot of fun creating the streamlit_book library. I hope you'll use it to create awesome books, courses, or presentations, and extend the ideas we started on the happy birds app. I'll keep updating the library and adding new features. You can check the documentation here and the source code here. If you create an app or want a new feature, reach out to me (in Spanish, English, or French)! Find me as @sebastiandres on Twitter and GitHub, or comment below!




Comments
Continue the conversation in our forums →